
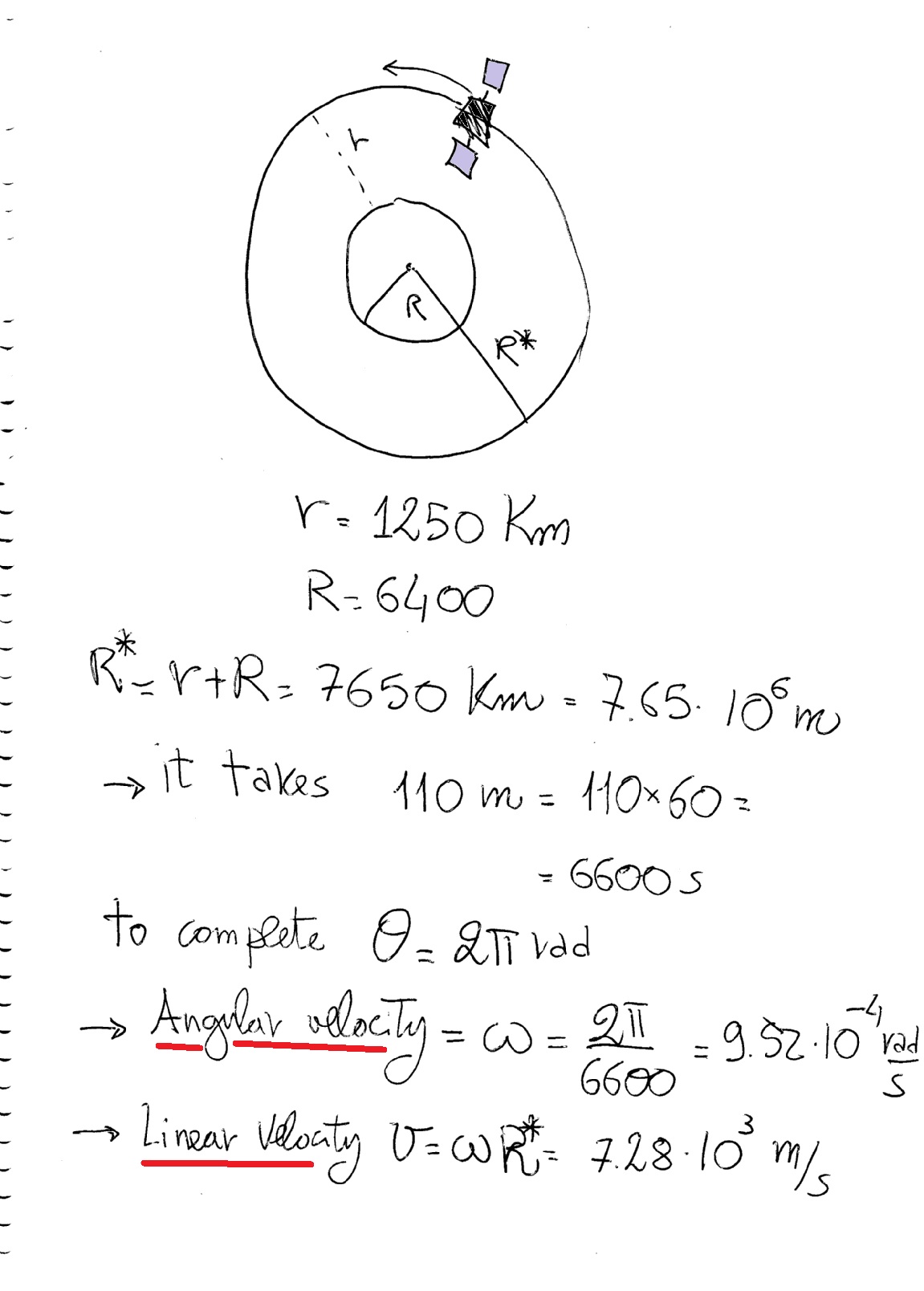
An end mass with measuring equipment of this tether system can be set directly on the moon’s surface. A new mission architecture is proposed, which includes three successive stages: initial deployment to the upper pulsation point (perigee), angular stabilization of the tether relative to the lower stable position, and maintaining a constant distance to a moon’s surface. As a result of eccentricity, the primaries move on ellipses around the barycenter, which rotates with angular velocity equal to that of the primaries, the position of the two-body pulsates along the axis connecting them. For the particular case when the tether is inextensible and two primaries moving in circular orbits about their mass center, these equations are integrated in quadrature, and the equilibrium positions and the oscillation period of the tether are found. The classical equations in the Nechville variables are converted into equations in polar coordinates. An orbiting spacecraft, which deploys the tether system, is located at the L1 libration point and is held at this point by the low thrust of its engines. The paper focuses on the study and development of a mission to use the L1 libration point for deployment of a tether system in the direction of a moon in the planar elliptic restricted three-body problem on the example of the Mars-Phobos system. In comparison with PID method and active disturbance rejection control method, simulation results demonstrate that the proposed control method has better tracking ability under airflow disturbances, specially gust. Finally, an extended state observer-based adaptive dynamic surface control approach is employed to guarantee the accurate tracking of the tethered aircraft under airflow disturbances.

Then, the system nonlinearity is handled by applying a new coordinate transformation, and the lumped disturbances are estimated by extended state observers. In this paper, by introducing the elasticity and length variation of the tether, the system model composed of the multi-link tether model and the 6-degree-of-freedom dynamics of the tether aircraft is accurately established, and the reachable domain of the tethered aircraft is carefully analyzed. Yet, due to the system nonlinearity, unknown airflow disturbances and unmeasurable tether tension, the anti-disturbance control of the tethered aircraft system is still a difficulty, which has not been well solved in the existing literature. Tethered aircraft system has been widely investigated because of its extensive application in hose-drogue autonomous aerial refueling, aerial towed decoy, and towed aerial recovery drogue, etc. The results of this study can be used to enable many future missions throughout the solar system. Conclusions about the feasibility of the implementation of the suggested mission and features of the behavior of the tether system using the proposed feedback control are made. Results of this simulation confirm the results obtained earlier. To validate the obtained results, numerical simulation of the space tether system controlled motion taking into account the eccentricity of the Mars–Phobos orbit using the equations in Nechvile's variables is performed. To provide asymptotic Lyapunov stability of the tether in the vicinity of equilibrium positions, the feedback control is proposed. Analytical formulas for the tether tension force are derived, and the influence of system parameters on this force is investigated for static and dynamic cases. For a constant-length tether, an energy integral, equilibrium positions, and phase portraits for various anchored point locations on the Phobos surface are found. The motion equations are derived in polar coordinates relative to the anchor point of the tether system. The basic assumptions in terms of a planar circular restricted three-body problem are formulated. The paper focuses on the development of a new mission to explore Phobos using an anchored tether system located below the L1 Mars–Phobos libration point and deployed toward Mars at a length slightly greater than the distance from Phobos.


 0 kommentar(er)
0 kommentar(er)
